IRRÉVERSIBILITÉ

IRRÉVERSIBILITÉ

L’irréversibilité est une caractéristique très générale des phénomènes d’évolution observés à notre échelle. Pour des conditions initiales données, un système évolue de manière irréversible lorsqu’il tend vers un état final unique, toujours le même, quel que soit son état initial. Il existe donc, dans ce cas, une direction d’évolution privilégiée qui ne peut être inversée sans l’action d’un agent extérieur au système.

Un exemple caractéristique est fourni par le phénomène de conduction thermique: si l’on met un corps à température élevée en contact avec un corps plus froid, la chaleur passera spontanément du corps chaud vers le corps froid. Ce processus se poursuit jusqu’à l’état final correspondant à l’égalité des températures. Le passage spontané de la chaleur du corps froid vers le corps chaud est impossible.

Le vieillissement biologique nous fournit une autre illustration bien tangible d’irréversibilité, liée ici aux réactions chimiques du métabolisme.

D’une manière générale, c’est l’existence de phénomènes irréversibles qui permet de fixer le sens d’écoulement objectif du temps.

L’irréversibilité en thermodynamique, conséquence du deuxième principe

Le deuxième principe de la thermodynamique codifie l’irréversibilité. Il se formule comme un bilan de la variation d’une fonction d’état du système, appelée l’entropie , communément désignée par la lettre S ^{[cf. ENTROPIE]}. La variation d S de l’entropie au cours d’une transformation du système peut toujours se décomposer en deux parties: la variation d ^e S due à l’échange d’énergie et de matière entre le système et le monde extérieur, et la variation d ⁱ S due à la création ou à la disparition d’entropie au sein du système:

Le deuxième principe de la thermodynamique se formule par l’inégalité:

Le signe d’égalité correspond à des transformations réversibles. Dès lors, dans tous les cas, les transformations irréversibles apportent une contribution positive à l’accroissement d’entropie. Donc l’entropie ne peut que croître dans un système par suite des transformations irréversibles qui s’y produisent. Dans un système isolé (d ^e S = 0), la croissance de l’entropie ne s’arrête que lorsque le système atteint l’équilibre thermique. L’entropie est donc un véritable «indicateur d’irréversibilité».

Tout en reconnaissant l’importance de l’irréversibilité, les thermodynamiciens classiques étaient plutôt gênés par son universalité. La raison en est la forme particulière du deuxième principe, qui se formule par une inégalité plutôt que par une équation. Les lois qui en résultent fixent des bornes (supérieures ou inférieures), mais ne permettent pas l’évaluation des valeurs exactes des grandeurs liées à l’entropie. Des énoncés thermodynamiques classiques sont du type: «Si la transformation de A à B était réversible, alors...», ou: «Si la transformation était infiniment lente, alors...» Autrement dit, dans l’ignorance de l’augmentation d’entropie, on devait délibérément se placer dans des conditions idéales, mais non réalisées en pratique, où d ⁱ S = 0.

Évaluation de la production d’entropie

Un grand progrès fut réalisé lorsque l’on réussit à évaluer explicitement la production d’entropie: on disposa dès lors d’une mesure quantitative des phénomènes irréversibles. Les grands noms liés à ces développements sont ceux de T. de Donder, L. Onsager, I. Prigogine.

Le point de départ de l’évaluation de la production d’entropie est une formule, due à J. W. Gibbs, qui relie la variation d’entropie d S à la variation d’énergie interne, à la variation de volume et aux vitesses des réactions chimiques qui se produisent dans le système. L’étape la plus importante consiste à combiner cette formule thermodynamique avec les lois d’évolution données par d’autres disciplines de la physique macroscopique: hydrodynamique, électrodynamique, cinétique chimique, etc. Ces lois fournissent des expressions explicites pour la variation d’énergie et pour les vitesses réactionnelles. Après quelques transformations simples, on arrive à écrire la variation de l’entropie sous la forme: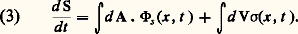

Le premier terme est l’intégrale, prise sur la surface du système, du vecteur flux d’entropie. Le deuxième terme, une intégrale de volume, représente la production d’entropie à l’intérieur du système. Cette équation correspond, terme à terme, à la relation (1), en donnant, de plus, des expressions explicites des grandeurs qui y figurent. Un examen de ces dernières montre que la production locale d’entropie a une forme très remarquable:

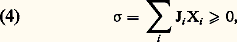où Xⁱ représente la force généralisée , cause du phénomène irréversible désigné par l’indice i ; Jⁱ représente le flux associé à ce phénomène. Par exemple, dans la conduction thermique, Xⁱ est proportionnel au gradient de la température, qui est la cause du flux de chaleur Jⁱ . La forme bilinéaire (4) doit être définie positive en vertu du second principe.

Lois linéaires et relations d’Onsager

Pour aller plus loin, il faut connaître les lois qui relient les flux aux forces généralisées: Jⁱ = Jⁱ (X). Si l’on se place suffisamment près de l’équilibre (où Xⁱ = 0 et Jⁱ = 0, 葉i ), on peut développer ces expressions en série et se limiter aux premiers termes:

Ce type de loi définit le domaine de la thermodynamique linéaire . Des cas particuliers en étaient connus depuis longtemps. Par exemple, la loi empirique de Fourier affirme que, dans un système siège d’un gradient de température (à l’exclusion de toute autre force), le flux de chaleur est proportionnel au gradient. Le coefficient de proportionnalité (dans cet exemple, la conductivité thermique) est un cas particulier des constantes L^ij , appelées coefficients de transport . Ces coefficients sont des grandeurs physiques très importantes, accessibles à la mesure expérimentale. Ils caractérisent la réponse du système envisagé aux stimuli extérieurs. L. Onsager a établi, en 1931, une loi fondamentale qui relie ces nombres entre eux: les coefficients de transport obéissent (en l’absence de champs magnétiques) aux relations de réciprocité:

Cette découverte a valu à Onsager le prix Nobel en 1968. Les relations (6) permettent de relier entre elles les caractéristiques de phénomènes très différents, et sont à la base d’un grand nombre de lois thermodynamiques (cf. THERMODYNAMIQUE – Processus irréversibles linéaires).

Les relations d’Onsager et les lois linéaires de même type ont cependant un domaine de validité limité. C’est seulement au cours des années 1960 que l’on a commencé à étudier systématiquement la thermodynamique non linéaire. Sans entrer dans les détails, signalons que, dans ce domaine, apparaissent des phénomènes tout à fait nouveaux et remarquables. Au fur et à mesure que l’on s’éloigne de l’équilibre, les régimes simples prédits par les lois linéaires deviennent instables, et le système «saute» sur d’autres branches d’évolution qui peuvent être totalement différentes. Il peut apparaître ainsi spontanément des structures spatiales ou des oscillations à partir de systèmes parfaitement homogènes au départ. Ces structures dissipatives jouent un rôle déterminant, aussi bien en hydrodynamique qu’en chimie et en biologie.

L’irréversibilité en mécanique statistique

La thermodynamique fournit des relations précieuses reliant entre eux des coefficients différents; elle ne permet pas de calculer la valeur de ceux-ci. Pour résoudre ce dernier problème, on fait appel à la mécanique statistique, dont le but est l’interprétation des phénomènes macroscopiques au moyen des propriétés et des mouvements des molécules. Mais, alors que le principe de l’étude des états d’équilibre était bien compris depuis longtemps, la théorie de non-équilibre s’est heurtée à des difficultés majeures, qui sont progressivement élucidées avec les découvertes de I. Prigogine.

Équation de Liouville

Considérons par exemple un gaz composé de N particules ponctuelles, qui sont enfermées dans un volume V, et qui interagissent. Si l’on admet que les lois de la mécanique classique sont une approximation suffisante (ce qui est souvent le cas dans ce type de problèmes), l’évolution du système est décrite par les 6N équations de Hamilton ^{[cf. STATISTIQUE]}, qui donnent la variation temporelle des 3N coordonnées qⁱ et des 3N moments conjugués pⁱ . À partir de ces équations, on déduit une équation unique qui gouverne la fonction de distribution F(q¹,..., q^N, p¹, ..., p^N ; t ). Celle-ci représente la densité de probabilité de trouver, à l’instant t , la particule 1 au point de coordonnées q¹ avec l’impulsion p¹, etc. L’équation d’évolution, appelée équation de Liouville , s’écrit: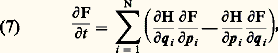

où H est l’hamiltonien du système. Cette équation est à la base de la mécanique statistique. Il est clair que cette équation ne change pas si l’on inverse le signe du temps et le signe des impulsions: t漣 t , pⁱ漣 pⁱ . Autrement dit, l’équation de Liouville décrit un mouvement réversible . Comment, dès lors, réconcilier la réversibilité fondamentale des mouvements des molécules avec l’irréversibilité observée à l’échelle macroscopique?

Théorie cinétique de Boltzmann

Historiquement, le premier modèle moléculaire d’un phénomène irréversible fut fourni par la théorie cinétique des gaz de L. Boltzmann, développée à la fin du XIX^e siècle. Cette théorie concerne la fonction de distribution réduite f ¹ (q, p; t ) (densité de probabilité de trouver une particule en q avec l’impulsion p, à l’instant t ). Celle-ci s’obtient à partir de F par intégration sur les variables de toutes les particules sauf une. Au moyen d’arguments semi-intuitifs, Boltzmann a établi une équation, qui porte son nom:

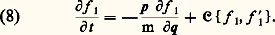Cette équation exprime le fait que, dans un gaz dilué, la variation temporelle de f ¹ est due (en l’absence de forces extérieures), d’une part, au mouvement libre des molécules (premier terme du second membre) et, d’autre part, aux collisions entre molécules, dont l’effet s’exprime par le terme non linéaire que l’on a schématisé par le symbole 暈f ¹, f ¹. L’équation (8) décrit une évolution irréversible. En particulier, Boltzmann a démontré le « théorème H », qui concerne une grandeur S (anciennement désignée par – H) définie comme suit:

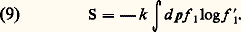Si l’on calcule la dérivée par rapport au temps de cette grandeur à l’aide de l’équation (8), on trouve une équation qui est exactement de la forme (3), avec 靖 閭 0. L’égalité est réalisée lorsque le gaz atteint l’équilibre thermique, caractérisé par la fonction de distribution de Maxwell. La grandeur S possède donc toutes les propriétés requises de l’entropie thermodynamique. La théorie de Boltzmann fait clairement apparaître les collisions comme la source de l’irréversibilité.

Dès sa publication, la théorie de Boltzmann s’est heurtée à des difficultés sérieuses. Celles-ci ont été cristallisées par les principaux critiques (J. J. Loschmidt, A. Zermelo) sous la forme de deux paradoxes célèbres.

Paradoxe de la récurrence . En vertu d’un théorème de H. Poincaré, tout système mécanique de dimension finie qui passe par une série d’états entre les instants t ¹ et t ² passera de nouveau dans un voisinage aussi petit que l’on veut de cette séquence après un temps fini. Il en résulte que l’entropie, définie par (9) comme une fonction d’état, ne peut pas être une fonction monotone croissante, mais doit être une fonction quasi périodique. Cependant, il est très important de noter que, pour tout système moléculaire réel, le temps de récurrence est tellement long qu’il dépasse toute imagination (10¹⁰¹⁰ années). À cause de cet ordre de grandeur, l’argument de la récurrence n’a pas grande valeur pratique.

Paradoxe de l’inversion des vitesses . Considérons un système mécanique qui évolue spontanément à partir d’un état initial et atteint un certain état au temps t = t ⁰. L’entropie correspondante augmente pendant ce temps. Imaginons qu’à l’instant t ⁰, on inverse exactement les vitesses de toutes les particules. À partir de cet état, le système retracera exactement le chemin parcouru précédemment et, à l’instant t = 2 t ⁰, il retrouvera sa condition initiale. Pendant ce temps, l’entropie du système doit diminuer, en contradiction avec le résultat de Boltzmann.

En réalité, la théorie cinétique de Boltzmann n’est pas une théorie mécanique exacte. Elle combine les lois du mouvement fournies par la mécanique avec des hypothèses probabilistes, justifiées par le grand nombre de particules et la grande complexité de leurs trajectoires. Boltzmann lui-même attira l’attention sur le caractère statistique du second principe de la thermodynamique: on peut aisément concevoir des situations où il peut être violé, mais la probabilité de ces situations est très faible dans un grand système. Malgré son caractère hybride, la théorie de Boltzmann fournit des résultats en excellent accord avec l’expérience. Il était donc naturel de rechercher la justification profonde de son succès.

La théorie statistique moderne de l’irréversibilité se donne pour objectif de généraliser les idées de Boltzmann et de résoudre – sans compromis – les paradoxes de l’irréversibilité dans le cadre de la mécanique statistique, classique ou quantique (cf. mécanique et thermodynamique STATISTIQUES).

irréversibilité [ irevɛrsibilite ] n. f.

• 1900; de irréversible

♦ Didact. Caractère de ce qui est irréversible. Irréversibilité du temps. Irréversibilité d'un cycle, d'une transformation énergétique. ⊗ CONTR. Réversibilité.

● irréversibilité nom féminin Propriété, caractère de ce qui est irréversible. Propriété d'une réaction chimique ou d'une transformation thermodynamique irréversibles. Propriété d'un mécanisme transmettant un mouvement d'un organe à un autre, sans qu'il soit possible à ce dernier de provoquer le mouvement du premier. ● irréversibilité (expressions) nom féminin Loi de l'irréversibilité, loi la plus générale de l'évolution, formulée en 1893 par le paléontologiste belge Louis Dollo (1857-1931) : « Lorsqu'un organe entre en régression, il ne peut plus faire retour en arrière et retrouver ce qu'il a perdu. »

⇒IRRÉVERSIBILITÉ, subst. fém.

Fait d'être irréversible, caractère de ce qui est irréversible; caractère irréversible de quelque chose. Dans le débat suraigu entre imprévisibilité et irréversibilité et dans l'unicité surfine qui en jaillit consiste tout le pathos de l'occasion (JANKÉL., Je-ne-sais-quoi, 1957, p. 131).

A. — [Correspond à irréversible A] Irréversibilité d'un cycle :

• 1. Comme le temps physique, le temps physiologique est irréversible. En réalité, il possède la même irréversibilité que les processus fonctionnels dont il est fait. Chez les animaux supérieurs, il ne change jamais de sens. Mais il se suspend de façon partielle chez les mammifères hibernants.

CARREL, L'Homme, 1935, p. 203.

— Spécialement

1. MÉCAN. L'irréversibilité du mouvement (...) n'était due qu'au frottement de la vis et des ses pivots (CHAMPLY, Nouv. encyclop. prat., t. 4, 1927, p. 26).

2. THERMODYN. Si le principe de Carnot n'est qu'un cas particulier du passage d'un mouvement d'une forme à une autre forme, il constitue bien, cependant, un phénomène de dégradation, à cause de l'irréversibilité pratique de ce passage (RUYER, Esq. philos. struct., 1930, p. 64).

B. — [Correspond à irréversible B] :

• 2. À ne considérer que deux unités économiques nous dirons que A exerce un effet de domination sur B, quand (...) A exerce une influence déterminée sur B sans que la réciproque soit vraie ou sans qu'elle le soit au même degré. Une dissymétrie ou irréversibilité de principe ou de degré est constitutive de l'effet en examen.

PERROUX, Écon. XX^e s., 1964, p. 30.

Prononc. : [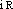()]. Étymol. et Hist. 1900 (BERGSON, Rire, p. 90). Dér. de irréversible; suff. -(i)té. Fréq. abs. littér. : 49.

irréversibilité [i(ʀ)ʀevɛʀsibilite] n. f.

ÉTYM. 1900, Bergson; de irréversible.

❖

♦ Didact. Caractère de ce qui est irréversible. || L'irréversibilité d'un cycle, d'un processus.

0 Comme le temps physique, le temps physiologique est irréversible. En réalité, il possède la même irréversibilité que les processus fonctionnels dont il est fait.

Alexis Carrel, l'Homme, cet inconnu, V, III.

♦ Phys. || Irréversibilité d'un mouvement; d'une transformation énergétique.

❖

CONTR. Réversibilité.

Encyclopédie Universelle. 2012.